- {{item.name}}
Arcusfunctions (反三角函数)指令库及其使用





- 0
- 139
Arcusfunctions (反三角函数)指令库及其使用
在 STEP 7 Micro/Win 软件的标准指令集中的浮点数运算指令中,已经提供了 sin(正弦),cos(余弦),tan(正切)三个正三角函数。如果用户需要使用反三角函数运算,可以使用下列“Arcusfunctions指令库”,指令库包含了 ARCTAN(反正切),ARCCOS(反余弦),ARCSIN(反正弦)三个运算指令。
添加 Arcusfunctions (反三角函数)指令库
点击上面的链接下载 反三角函数指令库到本地计算机硬盘,建议保存在 Micro/WIN 安装目录的 Lib 文件夹中。以下是一个完整路径的例子:
C:\Program Files\Siemens\STEP 7-Micro/WIN V4.0\Lib
然后将指令库库手动添加到 Micro/WIN 软件中。
 参见添加指令库。
参见添加指令库。
成功添加指令库后,用户可以在 STEP7 Micro/win 的指令树中找到:Arcusfunctions(v1.0)
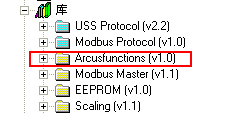
图 1. 反三角函数指令库
Arcusfunctions 指令库的应用
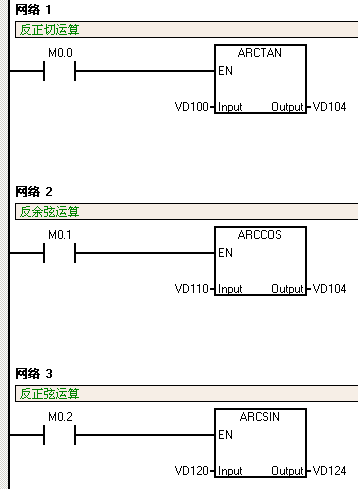
图 2. 反三角函数库编程举例
| 库指令 | 功能 |
| ARCTAN | 反正切运算 |
| ARCCOS | 反余弦运算 |
| ARCSIN | 反正弦运算 |
| 参数 | 数据类型 | 注释 |
| EN | BOOL | 信号为‘1’时激活库指令 |
| Input | REAL | 反三角函数值(即反正切,反余弦,反正弦值) |
| Output | REAL | 角度值(以弧度为单位) |
常问问题:
弧度与角度如何换算?
π = 180°
常用的三角函数公式
1. 同角三角函数的基本关系式
| tanα ·cotα=1 | sinα/cosα=tanα=secα/cscα | sin2α+cos2α=1 |
| sinα ·cscα=1 | cosα/sinα=cotα=cscα/secα | 1+tan2α=sec2α |
| cosα ·secα=1 | | 1+cot2α=csc2α |
2. 诱导公式:
| sin(-α)=-sinα | cos(-α)=cosα | tan(-α)=-tanα | cot(-α)=-cotα |
| sin(π/2-α)=cosα | cos(π/2-α)=sinα | tan(π/2-α)=cotα | cot(π/2-α)=tanα |
| sin(π-α)=sinα | cos(π-α)=-cosα | tan(π-α)=-tanα | cot(π-α)=-cotα |
| sin(3π/2-α)=-cosα | cos(3π/2-α)=-sinα | tan(3π/2-α)=cotα | cot(3π/2-α)=tanα |
| sin(2π-α)=-sinα | cos(2π-α)=cosα | tan(2π-α)=-tanα | cot(2π-α)=-cotα |
| sin(π/2+α)=cosα | cos(π/2+α)=-sinα | tan(π/2+α)=-cotα | cot(π/2+α)=-tanα |
| sin(π+α)=-sinα | cos(π+α)=-cosα | tan(π+α)=tanα | cot(π+α)=cotα |
| sin(3π/2+α)=-cosα | cos(3π/2+α)=sinα | tan(3π/2+α)=-cotα | cot(3π/2+α)=-tanα |
| sin(2kπ+α)=sinα | cos(2kπ+α)=cosα | tan(2kπ+α)=tanα | cot(2kπ+α)=cotα |
| | | | 其中k∈Z |
3. 两角和差公式:
sin(α+β)=sinαcosβ+cosαsinβ
sin(α-β)=sinαcosβ-cosαsinβ
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
tan(α+β)=( tanα+tanβ ) / ( 1-tanα ·tanβ )
tan(α-β)=( tanα-tanβ ) / ( 1+tanα ·tanβ )
4.万能公式
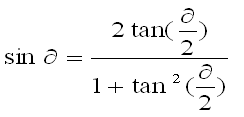

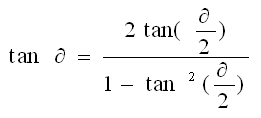
 以上三角函数公式均为抄录,如有差错,以数学书为准! 如需更多公式,请自行参考相关书籍。
以上三角函数公式均为抄录,如有差错,以数学书为准! 如需更多公式,请自行参考相关书籍。
5. 特殊三角函数值


剩余80%未阅读,请登录查看大全章节内容
- 评论
-
分享
扫码分享
- 收藏 收藏
- 点赞 点赞
- 纠错 纠错













 西门子官方商城
西门子官方商城


















{{item.nickName}}